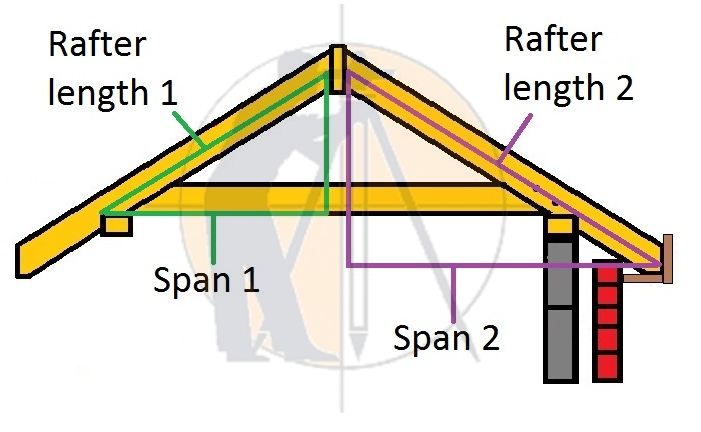
How To Calculate The Length Of Roof Rafters
Let us calculate the length of the roof rafter as shown in the below drawing.
The length of the roof rafters is calculated in three different methods based on the available data. Let us go through, all of them as explained below.
1. Roof rafter with pitch:
Given data:
Span = 20 ft.
Pitch = 7 /12
As you know,
Run = [span ÷ 2]
= [ 20 ft. ÷ 2]
= 10 ft.
Learn More
-
Size Of Aggregate Used In RCC, PCC, Slab, Road, Bridge And Dams
-
Why Crank Bars Are Provided In The Slab Construction
-
How To Calculate The Cement Bags Required For 2000 sq. ft. House
Here,
Pitch = [rise / run.]
i.e. ( 7 / 12 ) = [ rise / 10 ft.]
By cross multiplication,
Rise = [ (7/12 ) × 10 ft.]
= 5.833 ft.
By Pythagoras theorem,
AB2= AC2 + BC2
i.e. rafter2= rise2 + run2
Rafter = √ rise2 + run2
Rafter = √ (5.833)2 + (10)2
= √ 34.027 + 100
= √ 134.027
= 11.577 ft.
Length of the roof rafter = 11.577 ft.
-
Roof rafter with an angle & span:
Given data :
Span = 20 ft.
Angle θ = 25°
As you know,
Run = [span ÷ 2]
= [ 20 ft. ÷ 2]
= 10 ft.
By trigonometry,
sinθ = opposite / hypotenuse
In the above triangle,
Side AB = rafter = hypotenuse
Side BC = run = opposite.
So,
Sin25° = [ 10 ft. ÷ hypotenuse]
0.4226 = [ 10 ft. ÷ hypotenuse]
By cross multiplying,
Hypotenuse = [10 ft. ÷ 0.4226 ]
= 23.663 ft.
The length of the roof rafter = 23.663 ft.
Learn More
How To Calculate The weight of Steel With Formula
3. Roof rafter with an angle & rise:
Given data :
Rise = 8 ft.
Angle θ = 25°
By trigonometry,
cosθ = adjacent / hypotenuse
In the above triangle,
Side AB = rafter = hypotenuse
Side AC = rise = adjacent.
So,
Cos25° = [ 8 ft. ÷ hypotenuse]
0.906 = [ 8 ft. ÷ hypotenuse]
By cross multiplying,
Hypotenuse = [8 ft. ÷ 0.906 ]
= 8.83 ft.
The length of the roof rafter = 8.83 ft.