Surveying & Architects A unique platform of Civil Engineering
How to Find Arc Length
An arc is any portion of the circumference of a circle. Arc length is the distance from one endpoint of the arc to the other. Finding an arc length requires knowing a bit about the Geometry of a circle. Since the arc is a portion of the circumference, if you know what portion of 360 degrees the arc’s central angle is, you can easily find the length of the arc.
Using Measurement of Central Angle in Degrees.
Set up the formula for arc length.
The formula is {\displaystyle {\text{arc length}}=2\pi (r)({\frac {\theta }{360}})}, where {\displaystyle r} equals the radius of the circle and {\displaystyle \theta } equals the measurement of the arc’s central angle, in degrees
Learn More
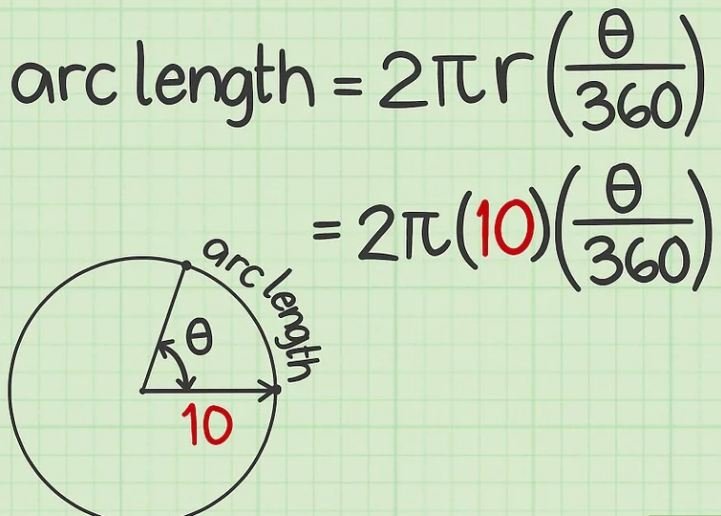
Plug the length of the circle’s radius into the formula.
This information should be given, or you should be able to measure it. Make sure you substitute this value for the variable {\displaystyle r}.
- For example, if the circle’s radius is 10 cm, your formula will look like this: {\displaystyle {\text{arc length}}=2\pi (10)({\frac {\theta }{360}})}.
Other Post
Plug the value of the arc’s central angle into the formula.
This information should be given, or you should be able to measure it. Make sure you are working with degrees, and not radians, when using this formula. Substitute the central angle’s measurement for {\displaystyle \theta } in the formula.
- For example, if the arc’s central angle is 135 degrees, your formula will look like this: {\displaystyle {\text{arc length}}=2\pi (10)({\frac {135}{360}})}.
Multiply the radius by 2π{\displaystyle 2\pi }.
If you are not using a calculator, you can use the approximation {\displaystyle \pi =3.14} for your calculations. Rewrite the formula using this new value, which represents the circle’s circumference.
- For example:
{\displaystyle 2\pi (10)({\frac {135}{360}})}
{\displaystyle 2(3.14)(10)({\frac {135}{360}})}
{\displaystyle (62.8)({\frac {135}{360}})}
Other Post
The Role And Responsibilities Of Quantity Surveyor In Current Construction Sectors
Divide the arc’s central angle by 360.
Since a circle has 360 degrees total, completing this calculation gives you what portion of the entire circle the sector represents. Using this information, you can find what portion of the circumference the arc length represents.
- For example:
{\displaystyle (62.8)({\frac {135}{360}})}
{\displaystyle (62.8)(.375)}
Multiply the two numbers together.
This will give you the length of the arc.
- For example:
{\displaystyle (62.8)(.375)}
{\displaystyle 23.55}
So, the length of an arc of a circle with a radius of 10 cm, having a central angle of 135 degrees, is about 23.55 cm.
Learn More
What is Scale Factor
Set up the formula for arc length.
The formula is {\displaystyle {\text{arc length}}=\theta (r)}, where {\displaystyle \theta } equals the measurement of the arc’s central angle in radians, and {\displaystyle r} equals the length of the circle’s radius.
Plug the length of the circle’s radius into the formula.
You need to know the length of the radius to use this method. Make sure you substitute the length of the radius for the variable {\displaystyle r}.
- For example, if the circle’s radius is 10 cm, your formula will look like this: {\displaystyle {\text{arc length}}=\theta (10)}.
Learn More
How To Calculate The Height Of Any Buildings And An Objects Using With Theodolite
Plug the measurement of the arc’s central angle into the formula.
You should have this information in radians. If you know the angle measurement in degrees, you cannot use this method.
- For example, if the arc’s central angle is 2.36 radians, your formula will look like this: {\displaystyle {\text{arc length}}=2.36(10)}.
Multiply the radius by the radian measurement.
The product will be the length of the arc.
-
For example:
{\displaystyle 2.36(10)}
{\displaystyle =23.6}
So, the length of an arc of a circle with a radius of 10 cm, having a central angle of 23.6 radians, is about 23.6 cm.
Other Post
-
Transition Curve In Highways – Purpose-Requirements-Example
-
How To Find The Coordinates Of Point P With The Help Of Point A & B
-
How To Calculate The Horizontal Distance Using With Auto Level Machine
