Surveying & Architects A unique platform of Civil Engineering
How to Convert Bearings And Distances to Coordinates
In This Article I will explain how to convert bearings and distance to coordinates.
Let’s Start,
Given a known Bearing (θ) & Horizontal Distance (Hz Distance) from a known point (Eo , No), the
coordinates (Ep , Np) may be calculated as follows:
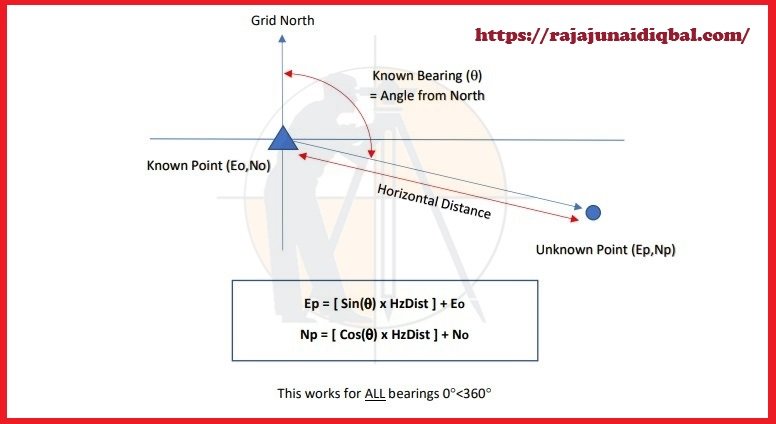
This works for ALL bearings 0°<360°
Hand Calculating
(1) It is important to carry out the above calculation in the correct sequence:
Sin(θ) x Hz Distance is not the same as Sin(θ x Hz Distance)
(2) Typing the above formulae into the Scientific Calculator, it may be necessary to enter the
bearing before the SIN/COS functions.
Eg, θ [SIN] [x] Hz Distance etc.
Microsoft Excel
The calculation may also be done using an Excel spreadsheet.
Note, that Excel assumes angles are measured in the “radians” & so the Bearing (measured in the
Degrees) must be converted using the “RADIANS(x)” function.
=(SIN(RADIANS(Bearing)) x Hz Distance)+East 0
=(COS(RADIANS(Bearing)) x Hz Distance)+North 0
Where “Bearing” is the known bearing in the degrees (or decimal degrees) and Hz Distance is the known
Horizontal Distance.
Learn More
Interview Question and Answer For Land Surveying
What is The Contour Mapping
Types Of Curves In Surveying Work
How to calculate the RL of temporary benchmark on the site
Rise and fall method with Examples
How to calculate The gradient, run and rise in civil construction
Example
Q: Calculate the coordinates of an unknown point measured from the Survey Station at known
coordinates (123.456mE, 456.789mN), given a measured Bearing of 127.5 degrees and the measured
Horizontal Distance of 34.567m?
A=
Easting=
Sin (127.5) = 0.79335334 Hint: U may need to enter 127.5 SIN on the calculator
x 34.567 = 27.42384491
+ 123.456 = 150.880m = East
B=
Northing=
Cos(127.5) = -0.608761429 Hint: Take care to note the “negative” sign
x 34.567 = –21.04305632
+ 456.789 = 435.746m = North
Note: The figures in RED show the “differences” in the position between the Survey Station & the
Unknown point. In this case, the point lies 27.424m to the EAST & 21.043m to the SOUTH of
Survey Station. As a check, this is where would expect the bearing 127.5 degrees to the point to.
